O DBSCAN (Density-Based Spatial Clustering of Applications with Noise) é um algoritmo que permite a detecção de aglomerados (clusters) em dados espaciais. Ao utilizar o conceito de densidade, o algoritmo permite detectar clusters de diferentes formatos. Por exemplo, considere que a posição dos veículos em uma cidade sejam representadas por pontos no espaço cartesiano. Neste caso, pode-se detectar um aglomerado de veículos, como um engarrafamento, que perpassa várias vias. Observe que o conceito que guia a detecção do aglomerado é a densidade, isto é, a quantidade de pontos espaciais em uma determinada localidade.
Para possibilitar esse processamento, o algoritmo recebe como entrada um conjunto de dados $D$ e utiliza dois parâmetros chave:
- $\varepsilon$ = o raio de densidade a ser considerado;
- $minPts$ = a quantidade mínima de dados dentro de um raio $\varepsilon$ para se formar um aglomerado (cluster).
Com base nesses conceitos, pode-se derivar o seguinte
- $N_{\varepsilon}(p)$ = o conjunto de dados que estão dentro de um raio $\varepsilon$ de distância do dado $p$.
Para exemplificar este conceito, considere a execução do algoritmo DBSCAN com os parâmetros $D = \{A,B,C,D,E,F,P\}$, $\varepsilon = 2$ e $minPts = 3$.
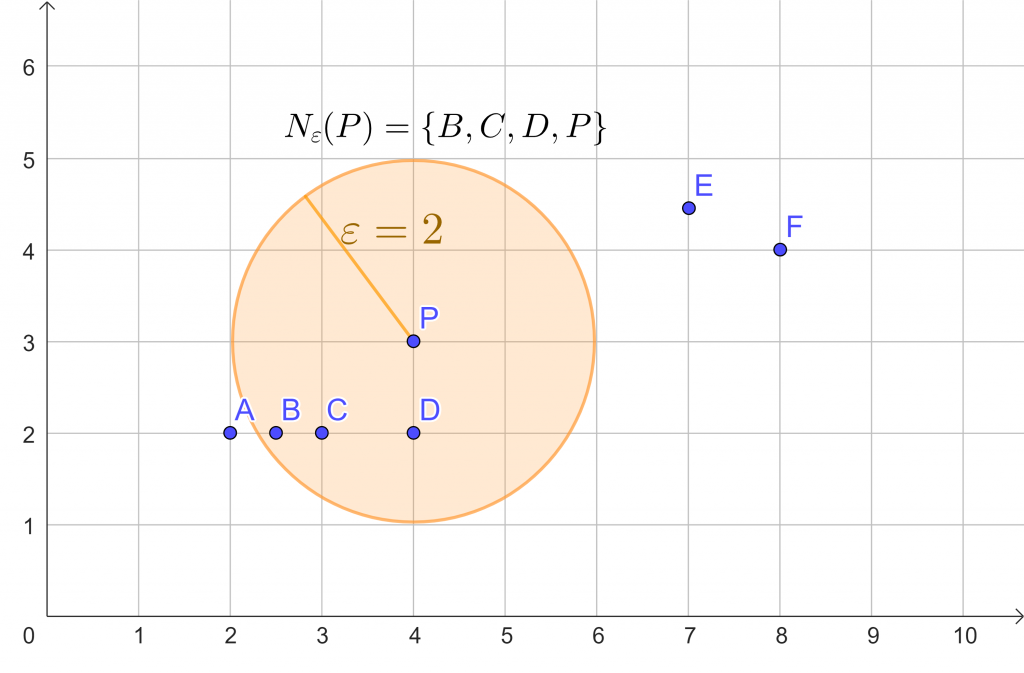
Neste caso, a vizinhança de $P$ é dada por $N_{\varepsilon}(P)=\{B,C,D,P\}$. Note que o próprio ponto $P$ faz parte de sua vizinhança. Como a vizinhança possui um valor maior ou igual a $minPts=3$, o algoritmo irá iniciar a detecção do cluster. Neste ponto, o algoritmo analisará todos os vizinhos de $P$, isto é, cria-se um conjunto $V$ a ser visitado com $N_{\varepsilon}(P)$. Para cada vizinho $Q \in V$, se $N_{\varepsilon}(Q) \geq 3$, explora-se os vizinhos de $Q$, isto é, adiciona-se $N_{\varepsilon}(Q)$ em $V$. Neste caso, o ponto $Q$ é conhecido como ponto de núcleo (core). Caso o vizinho $Q$ não possua o número mínimo de vizinhos, isto é, $N_{\varepsilon}(Q) < minPts$, os seus vizinhos não serão adicionados na exploração do cluster. No caso em questão, o ponto $Q$ será chamada de ponto de borda, uma vez que não expande o cluster. Após visitar todos os pontos de $V$ o algoritmo finaliza o cluster detectado e passa a processar os pontos restantes de $D$.
A rotina abaixa, $RangeQuery(D, p, \varepsilon)$ apresenta o algoritmo para detectar os vizinhos de um ponto $p$ da base de dados $D$. Note que esta é uma rotina computacionalmente cara, uma vez que requer uma comparação do ponto $p$ com todos os demais. Além disso, observe que o próprio ponto $p$ faz parte de $N_{\varepsilon}(p)$, uma vez que este conjunto inclui todos os pontos que estão a $\varepsilon$ de distância de $p$.
O algoritmo abaixo codifica a lógica do DBSCAN. Note que o algoritmo inicia o processamento dos dados da base de dados $D$. Quando se identifica um ponto de núcleo, linha 9, o algoritmo começa a expansão do cluster encontrado. Após exaurir a exploração, volta-se o processamento para os dados restantes, isto é, aqueles que não foram alcançados. Os pontos que não estão dentro do raio de alcance de um cluster são denominados como ruído (noise).
